An Angular Point of View: A Photo Collection Illustrating the History of Theodolites at the National Geodetic Survey
Used to measure horizontal and vertical angles, the theodolite remained the backbone of geodetic surveys from the 1800s until the early 1980s. This collection of theodolites tells the story of the development and usage of the instrument, including some of the challenges faced by field parties, from the first fieldwork of Survey of the Coast Superintendent Ferdinand Hassler until today.
- Introduction
- About this Collection
- Measuring Angles: Introduction
- A Brief History of "Turning Angles"
- Works Consulted
Introduction
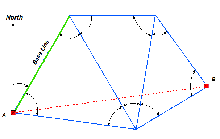
Point A to Point B by way of angles and a measured distance. Distances measured for scale are referred to as base lines. Click image for larger view.
Everyone has seen them - surveyors at a construction site or along a highway pointing what looks like a small telescope at a target. It is a small telescope, but they are not just looking at the scenery. Chances are, the surveyors are using a theodolite or transit to measure angles. By using the principles of trigonometry, the surveyors can use measured angles to figure out exactly where they are and where they (or the construction they are responsible for) are going.
As its name indicates, triangulation is a type of surveying largely based on the measurement of angles and distances, which build a series of connected triangles from which the latitude and longitude (or plane coordinates) for points of the triangle are derived.
Geodetic surveyors observe a star that has a known celestial position to determine a starting orientation. Then, by carefully measuring a distance for scale, they can use the series of interconnected triangles to map and model the surface of the continent from coast to coast. This is exactly what the Survey of the Coast (and its descendants) has done…and then some!
About this Collection
This collection of eight images illustrates some of the history of the theodolite, an instrument that combines a fine-quality telescope with a finely subdivided circle that allows the reading of angle values as the telescope is turned.
Used to observe both horizontal angles to build triangles and vertical angles to determine elevations, the theodolite remained the backbone of geodetic surveys from the first fieldwork of the Survey of the Coast in the 1800s until today's National Geodetic Survey (NGS) largely replaced triangulation and traverse work with global positioning system (GPS) surveys in the early 1980s. Theodolites are still an essential part of the "total" of the "total stations" used by crews of NGS's Aeronautical Survey Program and by many private surveyors.
The following collection of theodolites tells some of the story of the development and usage of the instrument, including some of the challenges faced by field parties, from the first fieldwork of Survey of the Coast Superintendent Ferdinand Hassler until today.
You can browse through the instruments in the collection by clicking on the links to the right or click here to view the items in the Theodolites Collection.
Measuring Angles: Introduction
Those who remember their high school geometry will find the core of geodetic surveying familiar: given a certain amount of information about the angles and lengths of the sides of a triangle, it is possible to calculate the remaining unknown lengths and angles of the triangle. Given this information and a beginning point whose coordinates are already known (X, Y in plane coordinates and on the high school pop quiz; latitude and longitude at NGS), it is possible to build a framework that allows the calculation of new points by the measurement of new angles and distances.
Classical, non-GPS geodetic surveyors measured those angles and distances with highly accurate equipment and techniques and performed calculations based on the reality that the measurements were performed on the curved surface of the Earth.

Before the advent of electronic distance measuring instruments, surveyors used tapes made of an alloy called "invar," to measure base lines. Click image for larger view.
In classical surveying, a line-of-sight is necessary between stations, since it is necessary to carefully sight on or align with a target during measurements. Until the 1950s, when electronic distance measurement was adopted, it was also necessary to measure the distances on a line, called a base line, which had been carefully cleared, graded, and leveled. The distances were then measured by carefully moving metal bars or tapes, usually 5 to 50 meters in length, end-to-end along the complete distance of the base line. Precise measurements of base lines that were typically 6 to 12 miles in length would often take several weeks to complete.
Using a Theodolite
Basic use of a theodolite required that the instrument be mounted on a stable tripod or stand and be carefully plumbed over the survey station that was to be occupied and observed from. The theodolite was then leveled.

In this photo from 1915, one surveyor looks through the telescope of a theodolite while his partner records angle measurements. Click image for larger view.
The observer looked through the telescope and carefully aligned the vertical cross-hair with the left-most survey target. The horizontal circle was rotated so that it read just above zero when the cross-hairs were on this target. The circle was then locked in place and the direction indicated on the circle was read and recorded. After this reading was taken, the telescope was rotated clockwise until the cross-hair was aligned with a second target. This second direction was read from the circle and recorded. This procedure was repeated until all targets were observed and recorded. Then, the telescope was rotated 180 degrees around both axes. The same stations were observed again and the angle values recorded.
This entire procedure was one set of angles.
The two readings for each target were averaged to help eliminate systematic errors. The number of sets of angles observed depended on the precision of the survey work being performed. For first-order survey work, 16 sets were observed and averaged to determine the final angles. Directions exceeding a specified value from the mean were rejected and repeated.
Background: A Brief History of "Turning Angles"
We have been measuring angles for surveying and construction for centuries. In building the great pyramids, Egyptians used an instrument called a "groma" to measure angles. Records indicate that the Romans used these tools as well. Roman surveyors also used a device called a "dioptra," which was an instrument that had a circular plate marked in angles.
The instruments used for the measurement of angles have evolved considerably from the groma and dioptra, with the developmental emphasis on marking and reading the subdivisions used to determine angles. In 1571, Leonard Digges described a "theodolitus," which was not quite what we now understand as a theodolite: a divided circle and square having a compass in the center, it lacked the familiar telescope of today.
By the mid-1700s, the more familiar telescope mounted with a horizontal circle and vertical semi-circle was being produced. Hand crafted of brass, with the angles also scribed by hand, theodolites of the era are virtually works of art. However, because the angles were scribed by hand, they were only as accurate as the capabilities of the person who made them. This was critical: an error of one second in a triangle translates into one foot at a distance of 40 miles. Early theodolites had expected errors of several minutes.
Englishman Jesse Ramsden's mechanical dividing engine was an enormous leap forward when invented in 1773. With its higher production and accuracy, the dividing engine replaced the slowness and possibility of human error associated with hand scribing. The dividing engine dramatically increased the availability of precision surveying and navigation instruments and placed England in the forefront of the production of such instruments.
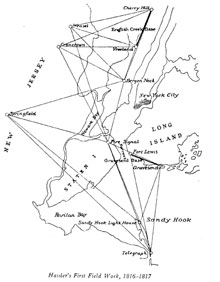
Hassler's first series of triangles. Note the extent of New York City in 1817. Secondary triangles were observed to fill in the map. Click image for larger view.
When Ferdinand Hassler was appointed Superintendent of the Survey of the Coast by Thomas Jefferson in 1807, he was already known for triangulation in his native Switzerland. When asked by Congress if another (cheaper) method than triangulation could be used to map the United States, Hassler replied with a thoroughly explained "No." He noted that many countries of Europe had already been mapped by triangulation, many before 1800.
It was to England that Hassler sailed with the blessings of Congress in August of 1811, seeking the best surveying equipment possible for the fledgling Survey of the Coast. He returned to the United States in October of 1815, having been stranded as an enemy alien during the War of 1812. He did, however, manage to obtain the high-quality instruments, many of his own design, he had sought.
Hassler's demand for the proper equipment to do the best job possible never faltered. His legacy, and the inventiveness and skill to design and build what could not be bought, was passed to the Coast and Geodetic Survey and still lives on today in its "descendent," the National Geodetic Survey.
Contributed by Cindy Craig, NOAA's National Ocean Service
Works Consulted
Bowie, W. (June 1932). The Standard Theodolite of the U.S. Coast and Geodetic Survey. Civil Engineering.
Hassler, F.R. (1820). Principle Documents Relating to the Survey of the Coast of the United States. Vol. I. (pp. 26 and 29).
House of Representatives Document 28, 27th Congress, 2nd Session, January 3, 1842. Response to question 15 (pp. 12-15).
Leiserowitz, A.A. The Dividing Engine in History [Electronic version]. Museum of Surveying Newsletter. Retrieved November 1, 2006, from: http://www.surveyhistory.org/the_dividing_engine1.htm.
Surveyor's Historical Society. Roman Surveying. Retrieved June 28, 2006, from: http://www.surveyhistory.org/roman_surveying1.htm.
University of Pennsylvania Corinth Computer project. Retrieved June 28, 2006, from: http://corinth.sas.upenn.edu/.
Wallis, D.A. (2005). History of Angle Measurement. Retrieved June 28, 2006, from: http://www.fig.net/pub/cairo/papers/wshs_01/wshs01_02_wallis.pdf.














